A propos "pressing a lever for food": Nobody would have to, if only the existing resources were equitably distributed. See Murray Bookchin's Post-scarcity anarchism (1986).
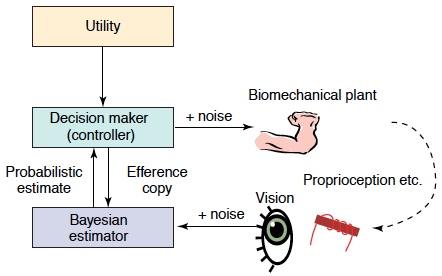
In general, optimizing motor performance is achieved through three classes of control:
Feedback controllers must only correct for variation that is deleterious to the task goal. Corrections of task-irrelevant errors are not only wasteful but they can also generate task-relevant errors.
This minimum intervention principle has now been demonstrated in a number of tasks including the seemingly simple task of generating a target force with the tip of the index finger. The control of this task can be characterized within a 7-dimensional space representing the seven muscles that regulate index finger force. The variability in this space can be partitioned into a task-relevant component that modulates force in the target direction and a task-irrelevant component that does not. During this task, task-irrelevant variability is consistently larger than task-relevant variability, suggesting that at the muscle level there is a preferential control of task-relevant dimensions.
[As Laozi's (rather extreme) version of this principle states, under maxim #48, "To conquer the world, accomplish nothing."]
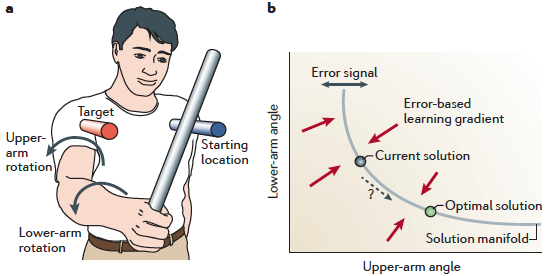
(a) A simple redundant task in which a target has to be reached
with a stick using two effectors: shoulder and arm, whose rotations
together contribute to a combined outcome.
(b) Many combinations of the two rotations will on average produce
the correct solution. The locus of these is the solution
manifold; the error signal corresponds to deviations from it (blue double arrow).
In contrast to an error signal, reinforcement signals — which can be as simple as "success" or "failure" — do not give information about the required control change. Thus, the learner must explore the possibilities to gradually improve its motor commands. Like error-based learning, RL can also be used to guide learning towards the solution manifold. However, because the signal (the reward) provides less information than in error-based learning (the vector of errors), such learning tends to be SLOW.
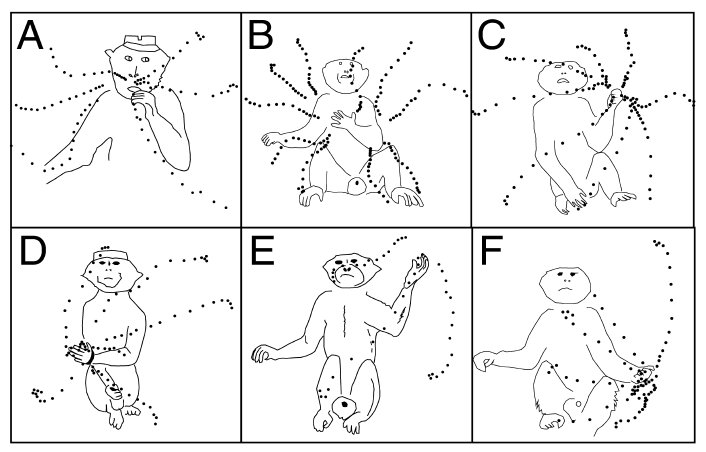
Motor control is HIERARCHICAL: some of the primitives (units) of action that it involves are very high-level.
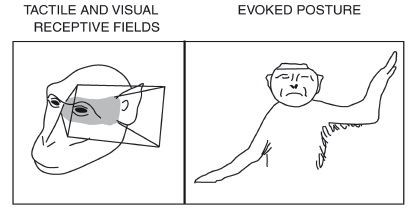
The illustration shows the postural MOVEMENT SYNERGIES evoked by stimulating single neurons in monkey precentral gyrus (from Graziano et al., 2002).
The zombie ant phenomenon shows what happens when
motor/action
 |
 |
Defense postures in monkey, man, and woman (the painting is a detail from Michelangelo’s Fall and Expulsion from Eden).
|
|
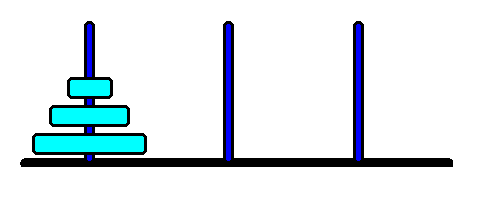
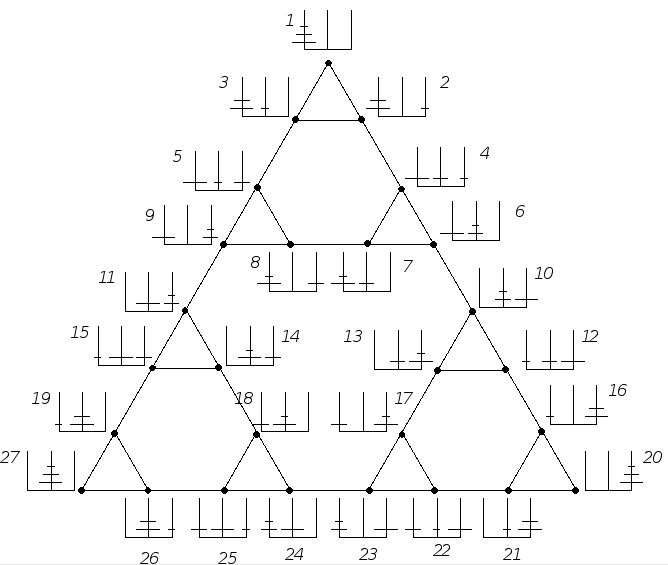
| The 3-disk version of the Towers of Hanoi problem... | ...and its STATE SPACE. |
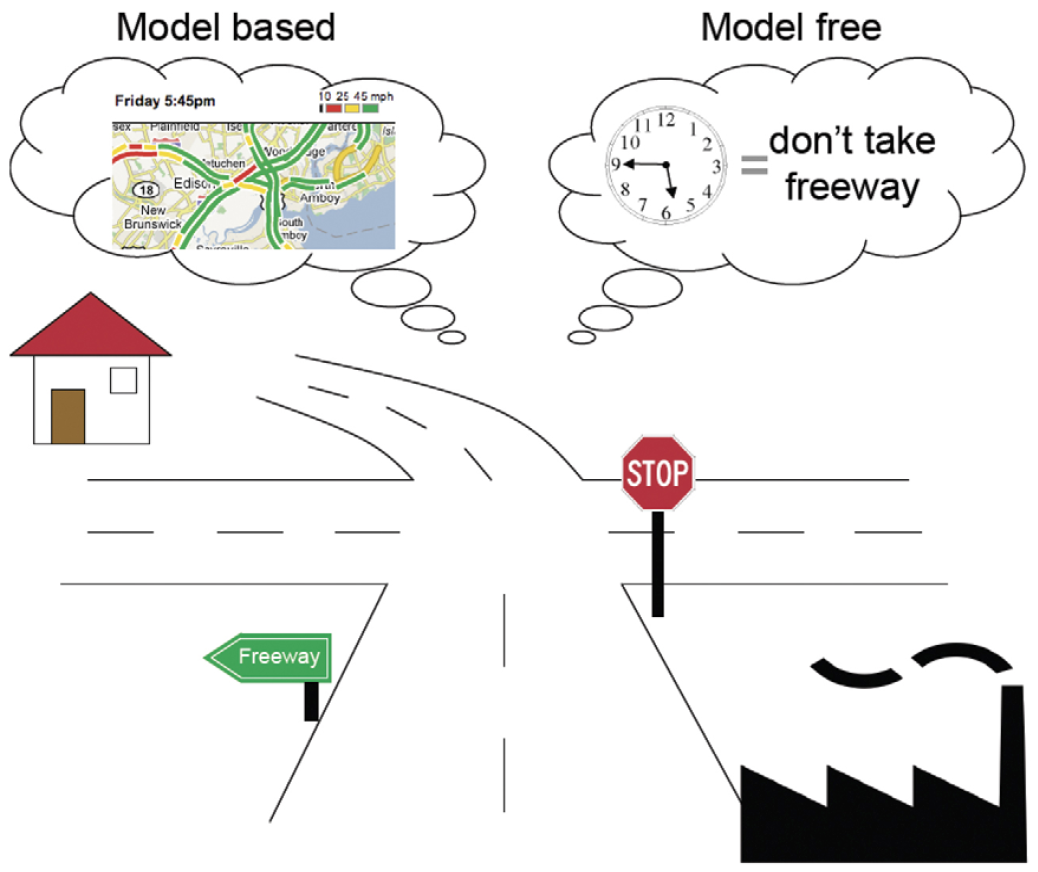Right: an illustration of the difference between model-free
and model-based approaches to decision-making.
Model-free vs. model-based RL,
from Theoretical Impediments to Machine Learning With
Seven Sparks from the Causal Revolution (2018) by the great
Judea
Pearl:
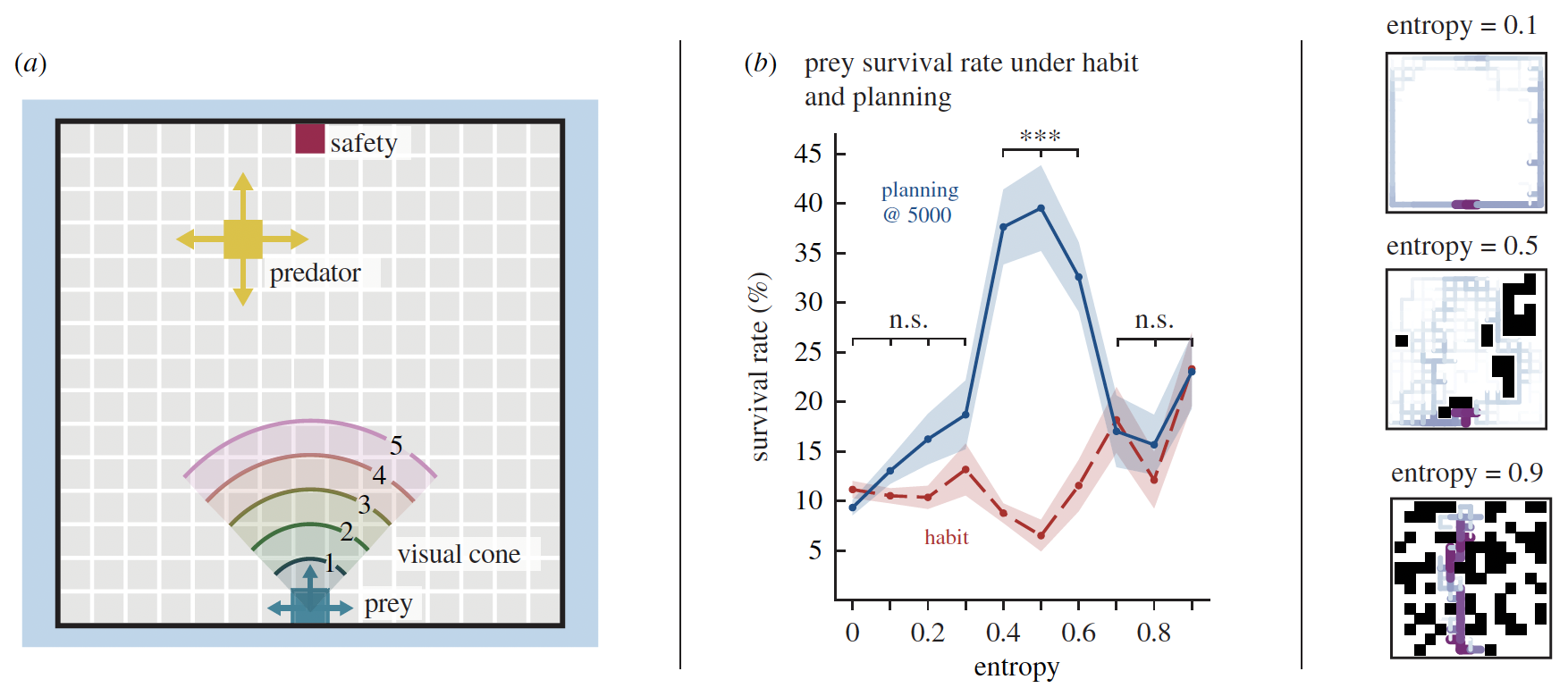
(a) Predator–prey simulations were performed in which the prey needed to reach the safety point without capture. The PREY’s action selection method varied between HABIT and PLANNING (the faster predator was always under a reactive controller to chase prey when seen, and search when not), visual range varied from short to unlimited, and obstacle density as quantified by entropy (black squares in b) varied from zero to high.
(b) Mid-entropy environments had the highest survival rates at the maximal degree of planning simulated. Low- and high-entropy environments performed no better under plan-based action selection than habit-based. On the right, occupancy frequency heat maps show that successful paths were stereotyped for low entropy and high entropy. In mid entropy, there was a high diversity of successful paths.
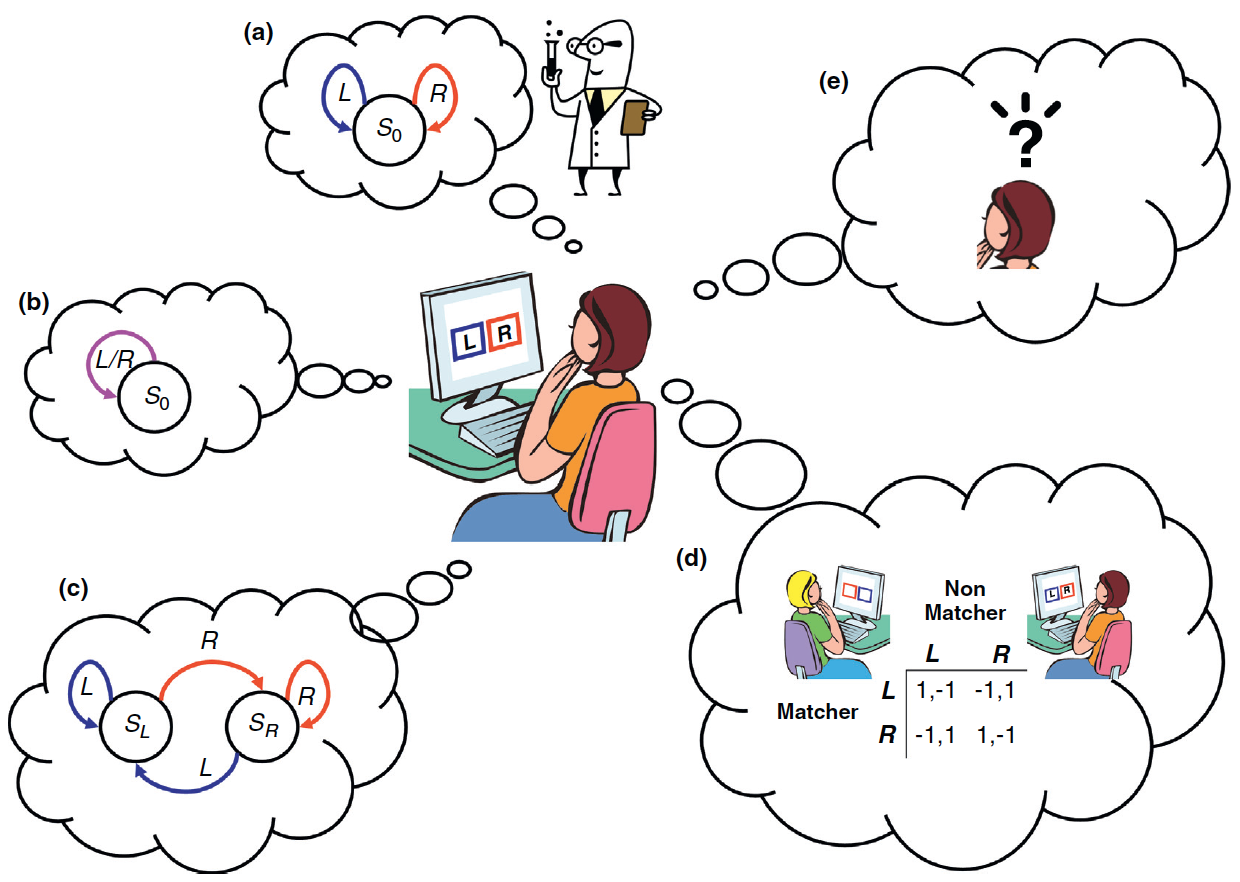
In this example, a participant is tested in the two-armed bandit task.
(a) From the experimentalist's point of view (scientist
caricature), the world is characterized by a single state (\(S_0\)) and two
actions: left (blue, L) or right (red, R) button press. However, from the
participant's point of view there is an infinite repertoire of possible
world models characterized by different sets of states and actions.
(b) With respect to the action sets, she may assume that there is
only a single available action, pressing any button, regardless of its
location (purple, L/R).
(c) With respect to the state sets, the participant may assume that
the state is defined by her last action (\(S_L\) and \(S_R\), for previous
L and R action, respectively).
(d) Moreover, the participant may assume she is playing a
penny-matching game with another human.
(e) These and other possible assumptions may
lead to very different predictions in the framework of RL.
If the RL task involves a video game, humans have a leg up over present-day AI in the form of sophisticated priors / world knowledge.
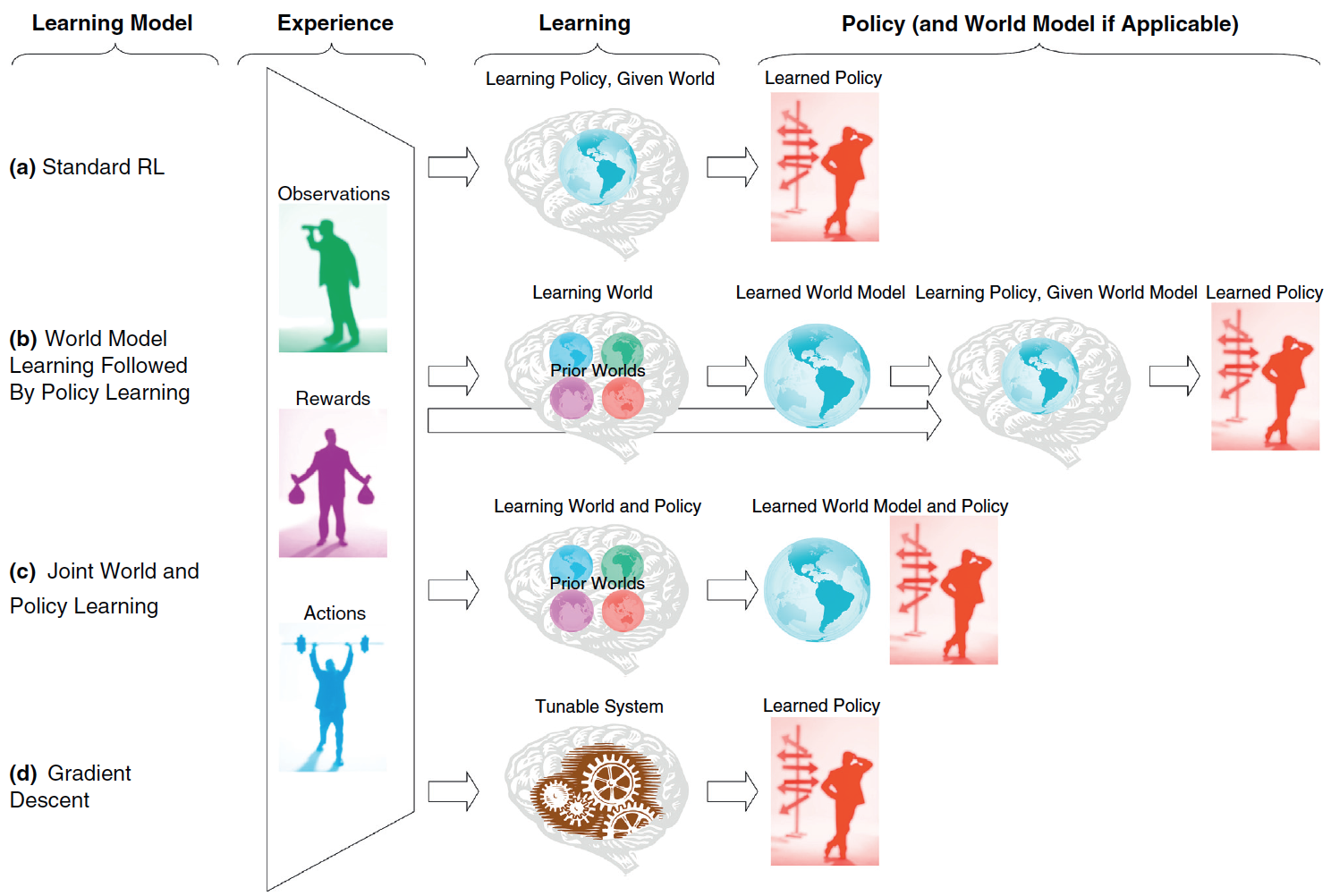
In operant learning, experience (left trapezoid), composed of present and past observations, actions and rewards, is used to learn a "policy".
(a) Standard RL models typically assume that the learner (brain gray icon) has access to the relevant states and actions set (represented by a bluish world icon) before the learning of the policy. Alternative suggestions are that the state and action sets are learned from experience and from prior expectations (different world icons) before (b) or in parallel (c) to the learning of the policy. (d) Alternatively, the agent may directly learn without an explicit representation of states and actions, but rather by tuning a parametric policy (cog wheels icon), for example, using stochastic gradient methods on this policy’s parameters.
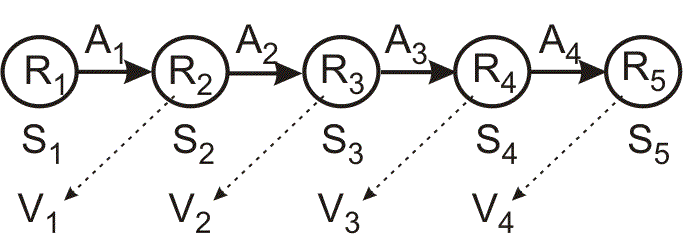
The best studied case is when RL can be formulated as a class of Markov Decision Problems (MDP).
The agent can visit a finite number of states \(S_i\). In visiting a state, it collects a numerical reward \(R_i\), where negative numbers may represent punishments. Each state has a changeable value \(V_i\) attached to it. From every state there are subsequent states that can be reached by means of actions \(A_{ij}\). The value \(V_i\) of a state \(S_i\) is defined by the averaged future reward \(\tilde{R}\) which can be accumulated by selecting actions from this particular state. Actions are selected according to a policy which can also change. The goal of an RL algorithm is to select actions that maximize the expected cumulative reward (the return) of the agent.
[For a useful introduction to RL, MDP, and the basic algorithms, see the Scholarpedia article.]
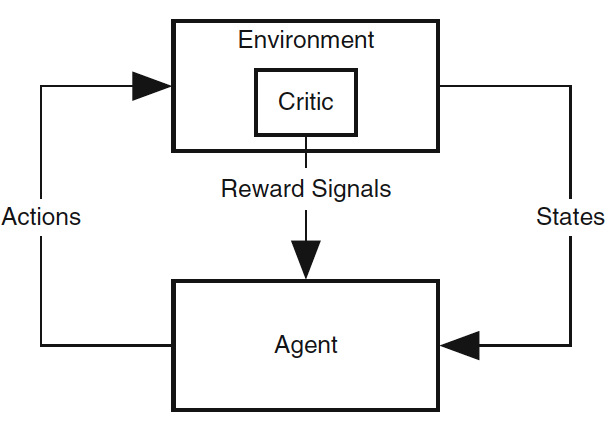
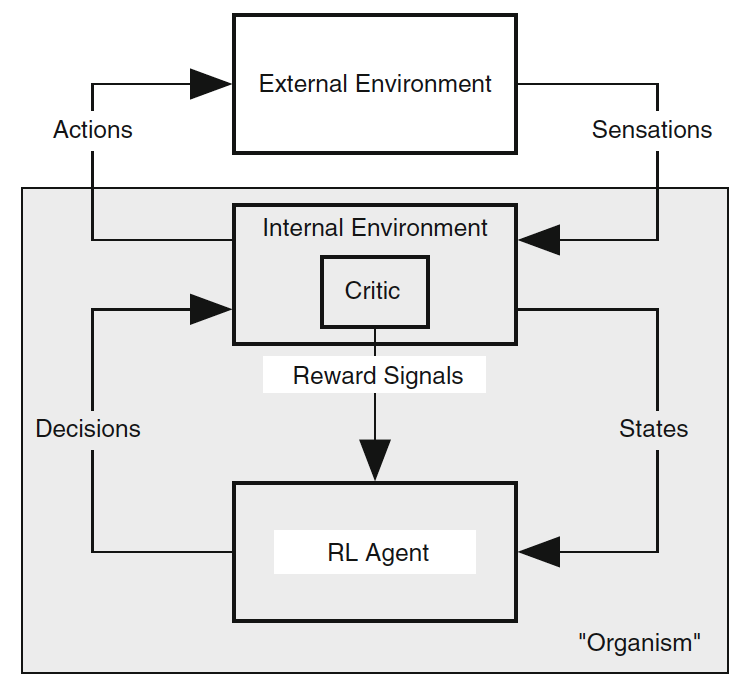
The old/standard view of agent-environment interaction in RL. Primary reward signals are supplied to the agent from a "critic" in its environment.
A refined view, in which the environment is divided into an internal and external environment, with all reward signals coming from the former. The shaded box corresponds to what we would think of as the "organism."
With this insight into the nature of the reward, the proper approach to RL is intrinsically motivated reinforcement learning.
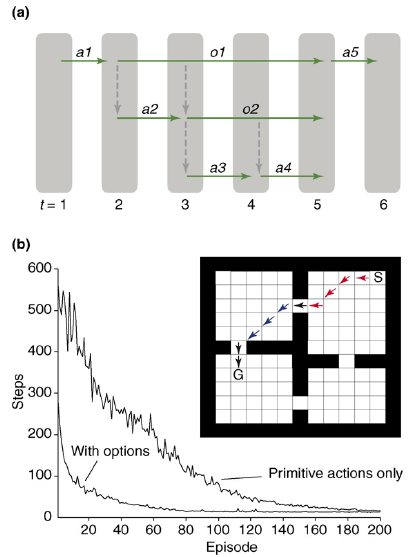
(a) A schematic of action selection in the OPTIONS framework. At the first time-step, a primitive action, a1, is selected. At time-step two, an option, o1, is selected, and the policy of this option leads to selection of a primitive action, a2, followed by selection of another option, o2. The policy for o2, in turn, selects primitive actions a3 and a4. The options then terminate, and another primitive action, a5, is selected at the top-most level.
(b) Inset: the rooms domain (Sutton et al.), as implemented by Botvinick et al.
S, start; G, goal. Primitive actions include single-step moves in the eight cardinal directions. Options contain policies to reach each door. Arrows show a sample trajectory involving selection of two options (red and blue arrows) and three primitive actions (black). The plot shows the mean number of steps required to reach the goal over learning episodes with and without inclusion of the door options.
Looking for optimal task hierarchy:
"Arranging actions hierarchically has well established benefits, allowing behaviors to be represented efficiently by the brain, and allowing solutions to new tasks to be discovered easily. However, these payoffs depend on the particular way in which actions are organized into a hierarchy[...] We provide a mathematical account for what makes some hierarchies better than others, an account that allows an optimal hierarchy to be identified for any set of tasks. We then present results from four behavioral experiments, suggesting that human learners spontaneously discover optimal action hierarchies."
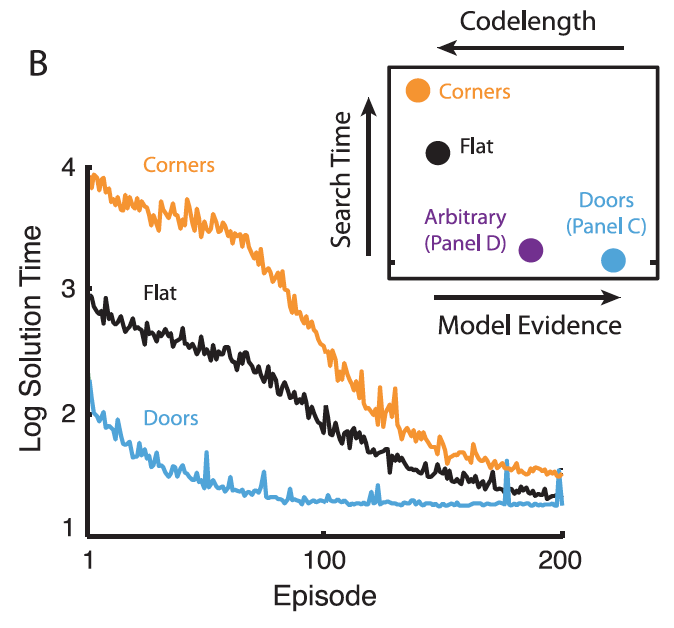
(B). Mean performance of three hierarchical reinforcement learning agents in the rooms task.
Inset: Results based on four graph decompositions. Blue: decomposition from panel C [previous slide]. Purple: decomposition from panel D. Black: entire graph treated as one region. Orange: decomposition with orange vertices in panel A segregated out as singleton regions.
Model evidence is on a log scale (data range \( -7.00 \times 10^4\) to \( -1.19 \times 10^5\)). Search time denotes the expected number of trial-and-error attempts to discover the solution to a randomly drawn task or subtask (geometric mean; range 685 to 65947; tick mark indicates the origin). Codelength signifies the number of bits required to encode the entire data-set under a Shannon code (range \(1.01\times 10^5\) to \(1.72\times 10^5\)). Note that the abscissa refers both to model evidence and codelength. Model evidence increases left to right, and codelength increases right to left.
In the present setting, where the models in question are different possible hierarchies, and the data are a set of target behaviors, the model evidence becomes: $$ P\left(behavior\mid hierarchy\right)=\sum_{\pi\in\Pi} P\left(behavior\mid hierarchy,\pi\right) P\left(\pi\mid hierarchy\right) $$ where \(\Pi\) is the set of behavioral policies \(\pi\) available to the candidate agent, given its inventory of subtask representations (this includes the root policy for each task in the target ensemble, as well as the policy for each subtask itself).
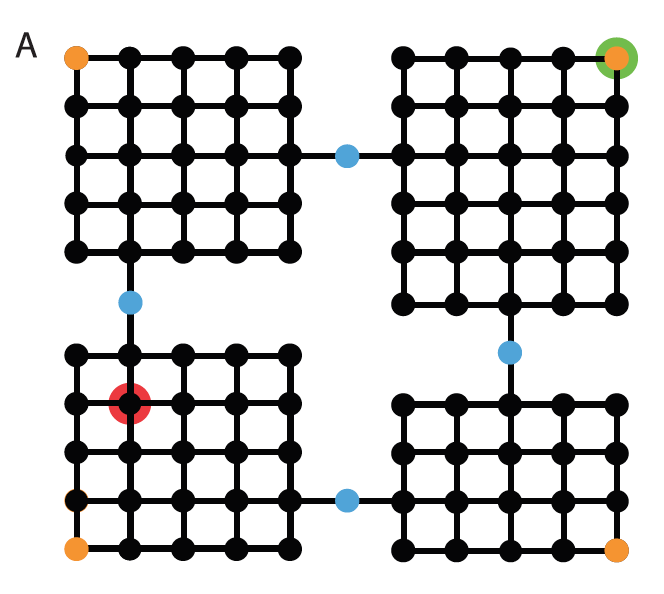
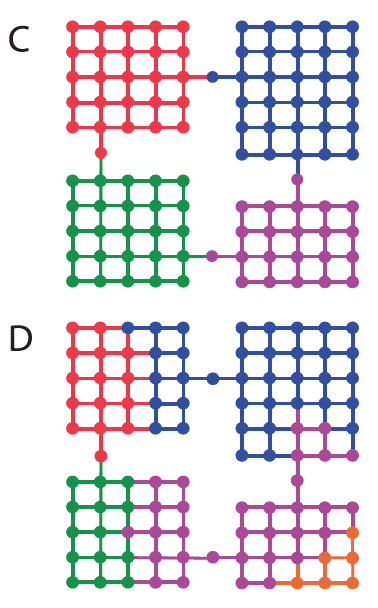
(C). Optimal decomposition. (D). An alternative decomposition.
(B). Task display from Experiment 1. A group of forty participants prepared to make a set of ‘‘deliveries’’ by learning the layout of a small town. The town comprised a set of ten locations, each associated with a distinctive visual icon. Participants were never given a bird’s eye view of the town. Instead, during an initial training period, participants were drilled on the adjacency relations among individual locations. Following this training period, participants were informed that they would next be asked to navigate through the town in order to make a series of deliveries between randomly selected locations, receiving a payment for each delivery that rewarded use of the fewest possible steps. Before making any deliveries, however, participants were asked to choose the position for a ‘‘bus stop’’ within the town. Instructions indicated that, during the subsequent deliveries, participants would be able to ‘‘take a ride’’ to the bus stop’s location from anywhere in the town, potentially saving steps and thereby increasing payments. Participants were asked to identify three locations as their first-, second- and third-choice bus stop sites.
(C). Graph employed in Experiment 1, showing the optimal decomposition. Width of each gray ring indicates mean proportion of cases in which the relevant bus stop location was chosen.
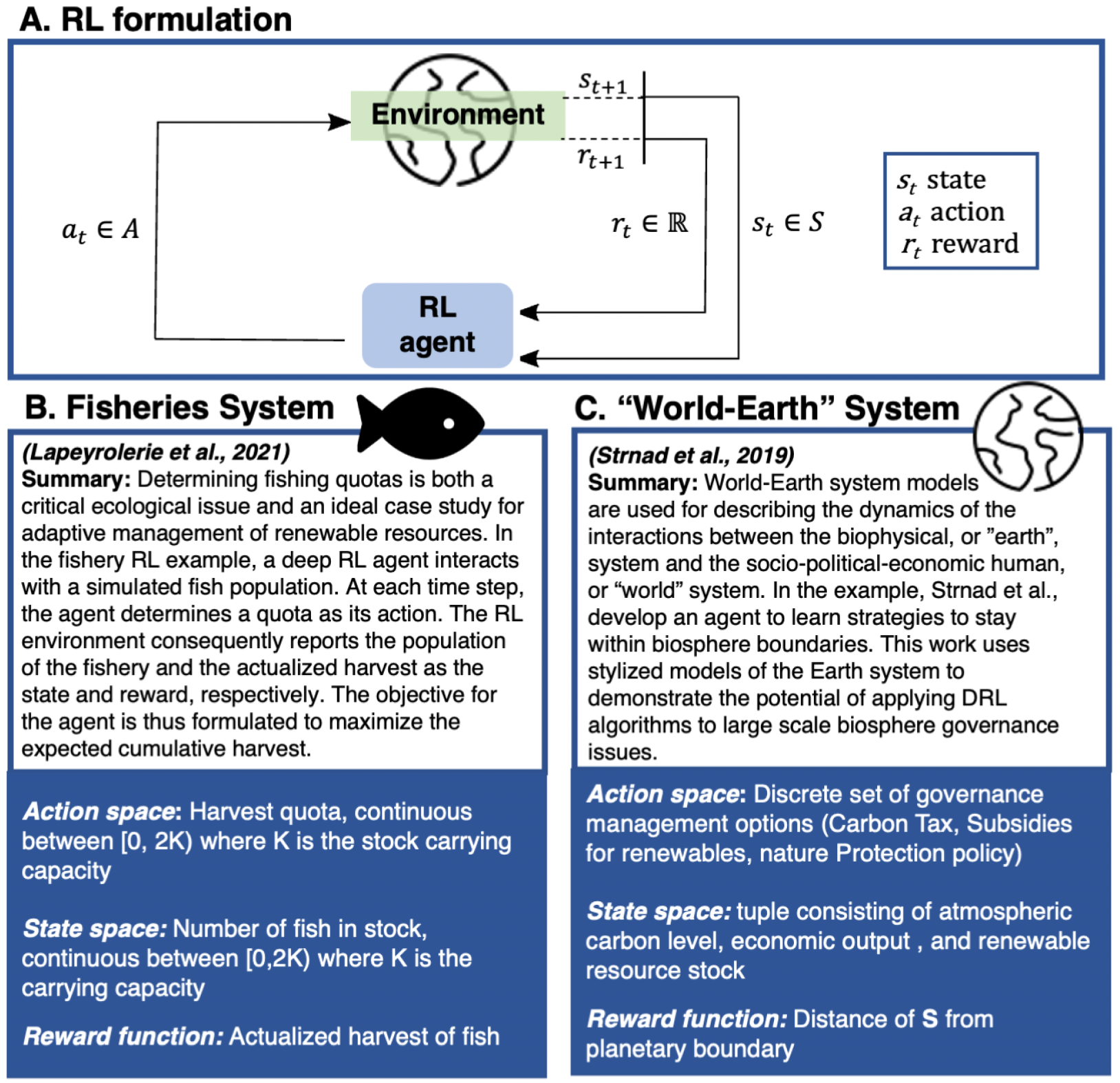
Which of the two formulations of RL in this real-life application would YOU prefer? HINT: focus on the reward function in each case.
How about NEITHER? Learn about the Indigenous concept of honorable harvest to see why.
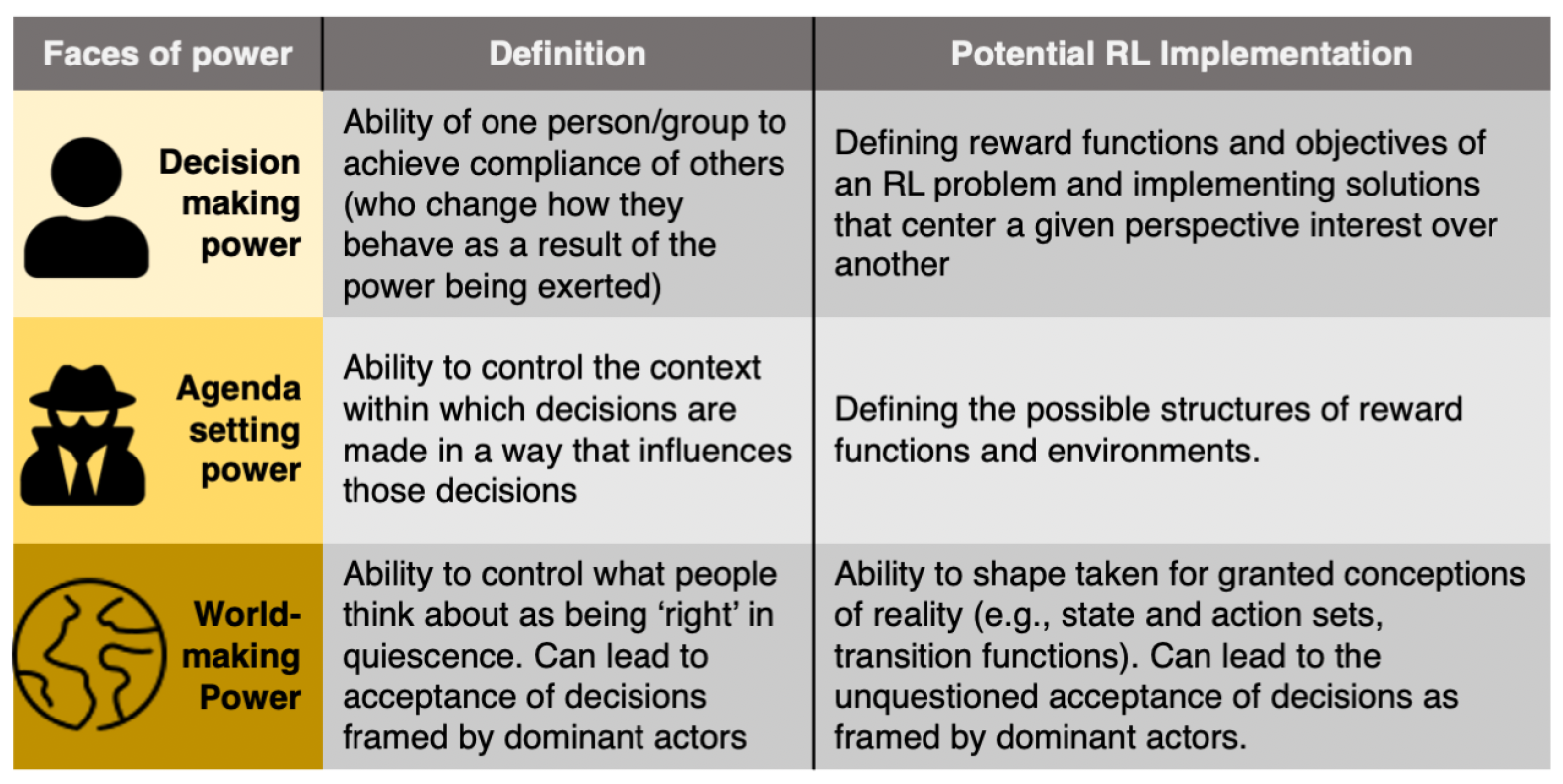
The concept of the three faces of power, applied to RL.