



























How and in what sense can the brain get to KNOW the world?
The control of behavior requires that the brain
perform MEASUREMENTS on the outside world.
Think of this is as intelligence-gathering for the sake of the command-and-control processes that reside in the War Room.
Any system trying to get to know the world through measurements must deal with UNCERTAINTY.
An aside: Consider the ethics of using WAR language in everyday life [as in "WAR ON DRUGS", a favorite phrase of copaganda peddlers]...
cui bono? ["who profits?"]


cui bono? ["who profits?"]
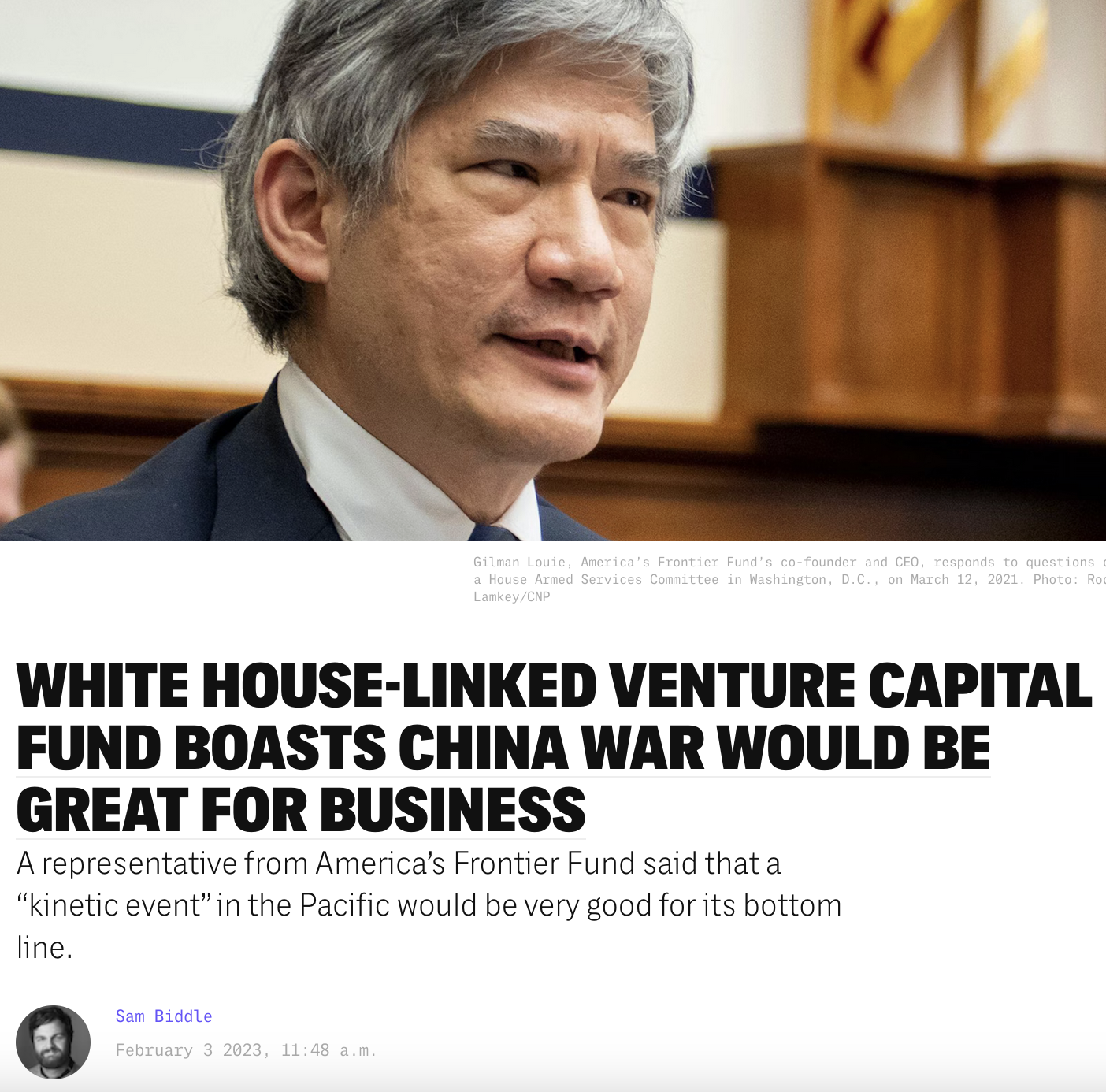
[from The Intercept_]
A war between China and Taiwan will be extremely good for business at America’s Frontier Fund, a tech investment outfit whose co-founder and CEO sits on both the State Department Foreign Affairs Policy Board and President Joe Biden’s Intelligence Advisory Board, according to audio from a February 1, 2024, event.
Gilman Louie, AFF’s co-founder and current CEO, serves as chair of the National Intelligence University, advises Biden through his Intelligence Advisory Board, and was tapped for the State Department’s Foreign Affairs Policy Board by Secretary of State Antony Blinken in 2022. Louie previously ran In-Q-Tel, the CIA’s venture capital arm.
"The key question that should be asked about any war is: who benefits from it? [...] The answer to this question is inconvenient, but hard to argue with: it is the power elites that reap a lion’s share of the material gain from war and that avoid most of its human toll; and it is the ordinary people on all sides who foot most of the bill. Perhaps instead of shyly thanking random military personnel at airports for their service, the children whom we encourage to do that should be taught to ask “What made you enlist?” and “Do you realize whose cause you serve?”"
How and in what sense can the brain get to KNOW the world?
Any system trying to get to know the world through measurements must deal with UNCERTAINTY. Therefore, the following observation is crucially important:
"All knowledge resolves itself into
The joint probability distribution $$ p(X,Y) $$ is the most that can be known about \(X\) and \(Y\) through observation.
[If you are allowed to intervene, you can
learn more, by doing
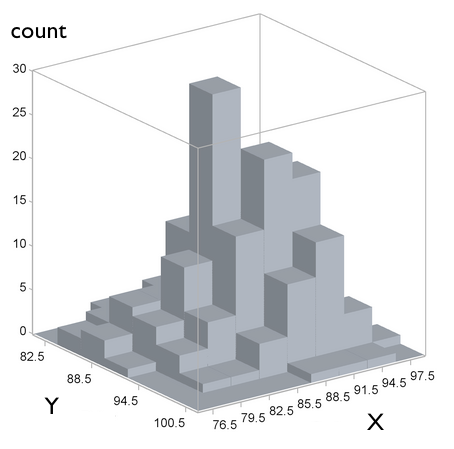
You can estimate \(p(X,Y)\) by dividing the range of \(X\) and of \(Y\) into bins and counting items that fall within each bin.
[Think of the values of \(X\) coding apple color; \(Y\) coding apple crunchiness.]
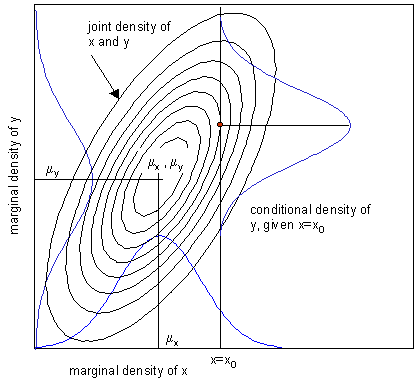
From the joint probability distribution function \(p(X,Y)\), one can compute the marginal distributions \(p(X)\) and \(p(Y)\).
Very importantly (from the applied standpoint, as we shall see), from these one can compute the conditional distributions. By definition of
$$
p(Y\mid X) = \frac{p(X,Y)}{p(X)} ~~~~~~~~~~~~~~~~ p(X\mid Y) = \frac{p(X,Y)}{p(Y)}
$$
If \(X\) and \(Y\) are
independent, then \(p(Y\mid X)=p(Y)\) and \(p(X\mid Y)=p(X)\).
An interactive visual demo illustrating conditional probability.

As an example, the
$$ P(OMGtasty \mid {\color{red} red}) = \frac{P(OMGtasty,{\color{red} red})}{P({\color{red} red})} $$
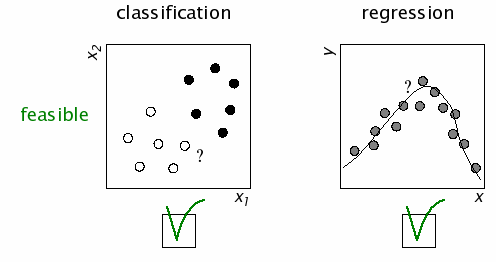
The computational essence of categorization and regression:*
1.
Example: categorization (given \(size\) and \(color\), predict \(crunchy/mushy\)).
1.
Example: estimation (given \(color\), predict \(HOW tasty\)); also
visual-motor coordination.
* NOTE: input/output or stimulus-response mapping (which includes categorization and regression) by no means covers everything that minds do to control behavior, but it is an indispensable conceptual starting point.
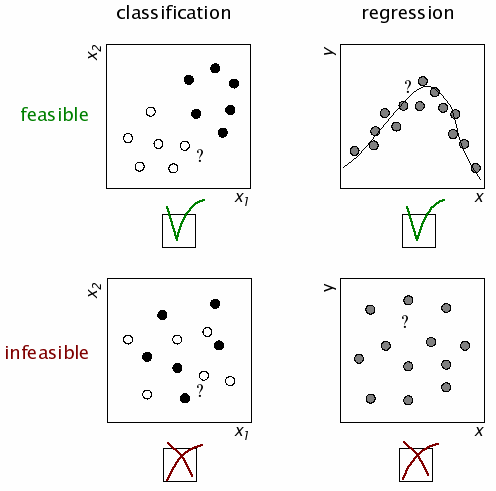
The computational essence of categorization and regression:
— Both classification and regression are
— Both require
Continuing the example of learning to deal with apples:
\(x_1\) : color dimension
\(x_2\) : size dimension
| from experience, we may know | \(p\left(x_1^{(Z)}, x_2^{(Z)} \mid {\cal C}_1\right)\) | — how often the crunchy apples \(Z\) we tasted happened to be of a particular color and size |
| but what we need to know is | \(p\left({\cal C}_1 \mid x_1^{(A)}, x_2^{(A)}\right)\) | — how likely an apple \(A\) of this color and size is to be crunchy (before tasting it) |
The Bayes Theorem shows the way.
 The
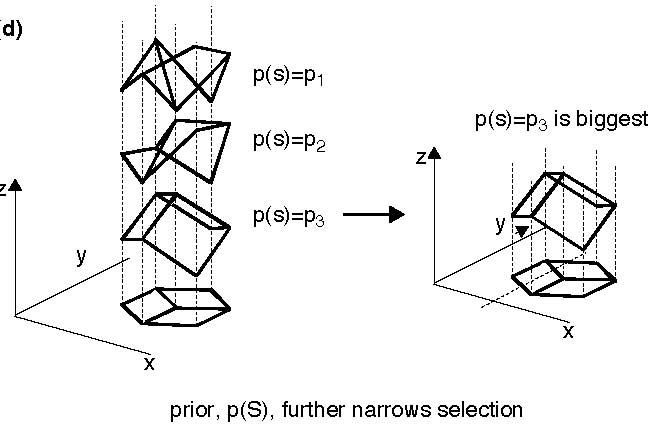
The 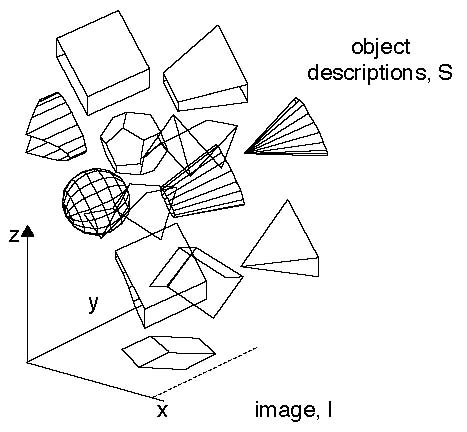 |
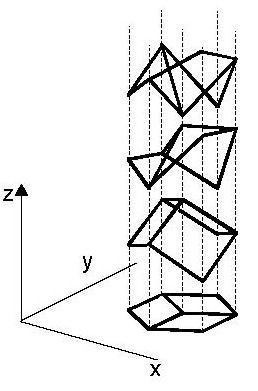 |
| Problem: find the probabilities of various conceivable shape interpretations (hypotheses), given the image (data). According to Bayes, $$p(S\mid I) \propto p(I\mid S)p(S)$$ | The likelihood term, \(p(I\mid S)\), rules out shapes \(S\) that are inconsistent with the image \(I\) (here, spheres, cones, etc.). |
"The brain is an information processor; and information processing typically involves inferring new information from information that has been derived from the senses, from linguistic input, or from memory. This process of inference from old to new is, outside pure mathematics, typically uncertain."
"Probability theory is, in essence, a calculus for uncertain inference, according to the SUBJECTIVE INTERPRETATION OF PROBABILITY.
Thus probabilistic methods have potentially broad application to
uncertain inferences:
— from sensory input to environmental layout;
— from speech signal to semantic interpretation;
— from goals to motor output;
— or from observations and experiments to regularities in nature."
"Crucially, the frequency interpretation of probability is not in play here — in cognitive science applications, probabilities refer to 'DEGREES OF BELIEF'.
Thus, a person's degree of belief that a coin that has rolled under the table has come up heads might be around 1/2; this degree of belief might well increase rapidly to 1 as she moves her head, bringing the coin into view. Her friend, observing the same event, might have different prior assumptions and obtain a different stream of sensory evidence.
Thus the two people are viewing the same event, but their belief states and hence their subjective probabilities might differ. Moreover, the relevant information is defined by the specific details of the situation. This particular pattern of prior information and evidence will never be repeated, and hence cannot define a limiting frequency."
"The subjective interpretation of probability generally aims to evaluate CONDITIONAL PROBABILITIES, \(Pr(h_j\mid d)\), that is, probabilities of alternative hypotheses, \(h_j\) (about the state of reality), given certain data, \(d\) (e.g. available to the senses). By Bayes' theorem, $$ Pr(h_j \mid d) = \frac{Pr(d \mid h_j) Pr(h_j)}{Pr(d)} $$ The centrality of Bayes' Theorem to the subjective approach to probability has led to the approach commonly being known as the Bayesian approach. But the real content of the approach is the subjective interpretation of probability; Bayes' Theorem itself is just an elementary, if spectacularly productive, identity in probability theory."
"Sophisticated probabilistic models can be related to cognitive processes in a variety of ways. This variety can usefully be understood in terms of Marr's celebrated distinction between three levels of computational explanation: the computational level, which specifies the nature of the cognitive problem being solved, the information involved in solving it, and the logic by which it can be solved; the algorithmic level, which specifies the representations and processes by which solutions to the problem are computed; and the implementational level, which specifies how these representations and processes are realized in neural terms.
Finally, turning to the implementational level, one may ask whether THE BRAIN ITSELF SHOULD BE VIEWED IN PROBABILISTIC TERMS. Intriguingly, many of the sophisticated probabilistic models that have been developed with cognitive processes in mind map naturally onto highly distributed, autonomous, and parallel computational architectures, which seem to capture the qualitative features of neural architecture."
Assume that we have an agent who is attempting to infer the process that was responsible for generating some data, \(d\). Let \(h\) be a hypothesis about this process, and \(P(h)\) — the prior probability that the agent would have accepted \(h\) before seeing \(d\). How should the agent's beliefs change in the light of the evidence provided by \(d\)? To answer this question, we need a procedure for computing the posterior probability, \(P(h \mid d)\). This is provided by the Bayes Theorem: $$ P(h \mid d) = \frac{P(d \mid h) P(h)}{P(d)} $$
How can the posterior be used to guide action?
The denominator is obtained by summing over [the mutually exclusive] hypotheses, a procedure known as marginalization: $$ P(d) = \sum_{h^{\prime}\in H} P(d \mid h^{\prime}) P(h^{\prime}) $$ where \(H\) is the set of all hypotheses considered by the agent.
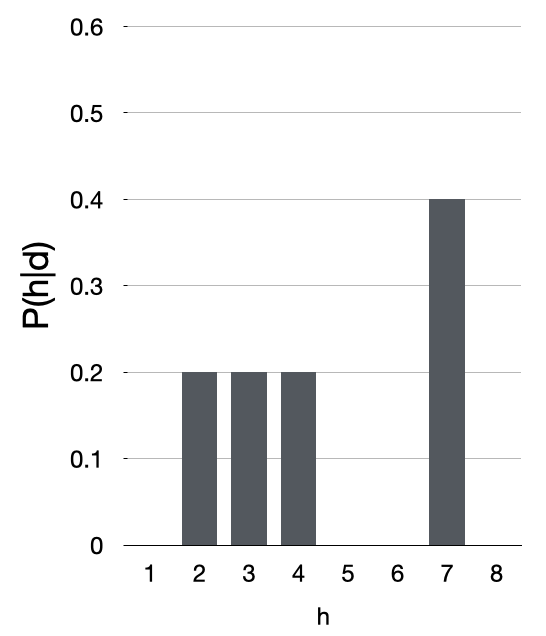
How can the posterior DISTRIBUTION be used to guide action?
If this is the posterior \(P(h \mid d)\) for a certain regression problem involving data \(d\), what value of \(h\) would you choose as the answer to the problem?
Bayesian decision theory introduces a loss function \(L\left(h, \alpha\left(d\right)\right)\) for the cost of making a decision \(\alpha(d)\) when the input is \(d\) and the true hypothesis [true state of affairs] is \(h\). It proposes selecting the decision function or rule \(\alpha^{\star}(\cdot)\) that minimizes the RISK, or EXPECTED LOSS: $$ R(\alpha) = \sum_{h,d} L\left(h, \alpha\left(d\right)\right) P(h, d) $$ or in words: weight the loss for each possible combination of data (which dictates a decision) and true hypothesis by how probable that combination is, and sum these resulting values. This is RATIONAL DECISION MAKING.
In classification, \(L\) can be chosen so that the same penalty is paid for all wrong decisions:
\(L\left(h, \alpha\left(d\right)\right) = 1\) if \(\alpha\left(d\right) \neq h\)
and
\(L\left(h, \alpha\left(d\right)\right) = 0\) if \(\alpha\left(d\right) = h\).
Then the best decision rule is the maximum a posteriori (MAP) estimator \(\alpha^{\star}(d) = \textrm{argmax}_{h} P(h \mid d)\).
Bayesian decision theory introduces a loss function \(L\left(h, \alpha\left(d\right)\right)\) for the cost of making a decision \(\alpha(d)\) when the input is \(d\) and the true hypothesis [true state of affairs] is \(h\). It proposes selecting the decision function or rule \(\alpha^{\star}(\cdot)\) that minimizes the RISK, or EXPECTED LOSS: $$ R(\alpha) = \sum_{h,d} L\left(h, \alpha\left(d\right)\right) P(h, d) $$ or in words: weight the loss for each possible combination of data (which dictates a decision) and true hypothesis by how probable that combination is, and sum these resulting values. This is RATIONAL DECISION MAKING.
In regression, the loss function can take the form of the square of the error:
\(L\left(h, \alpha\left(d\right)\right) = \left\{h−\alpha\left(d\right)\right\}^2\)
Then the best solution is the posterior mean, that is, the probabilistically weighted average of all possible (numerical in this case) hypotheses: \(\sum_{h} h P(h \mid d)\).
An important distinction: generative models vs. empirical risk minimization approaches —
In many situations, we will not know the distribution \(P(h, d)\) exactly but will instead have a set of labelled samples \(\left\{\left(h_i, d_i\right) : i = 1,\dots,N\right\}\). The risk $$ R(\alpha) = \sum_{h,d} L\left(h, \alpha\left(d\right)\right) P(h, d) $$ can then be approximated by the empirical risk, $$ R_{emp}(\alpha) = \frac{1}{N} \sum_{i=1}^{N} L\left(h_i, \alpha\left(d_i\right)\right) $$ Some methods used in machine learning, such as certain "neural networks" and support vector machines, attempt to learn the decision rule directly by minimizing \(R_{emp}(\alpha)\) instead of trying to model \(P(h, d)\).
More importantly for us, BRAINS may have evolved to apply either or both of these two approaches in the context of a particular class of tasks. The distinction between them is similar to the one between "model-based" and "model-free" reinforcement learning, which I'll discuss in Lecture 7.2.
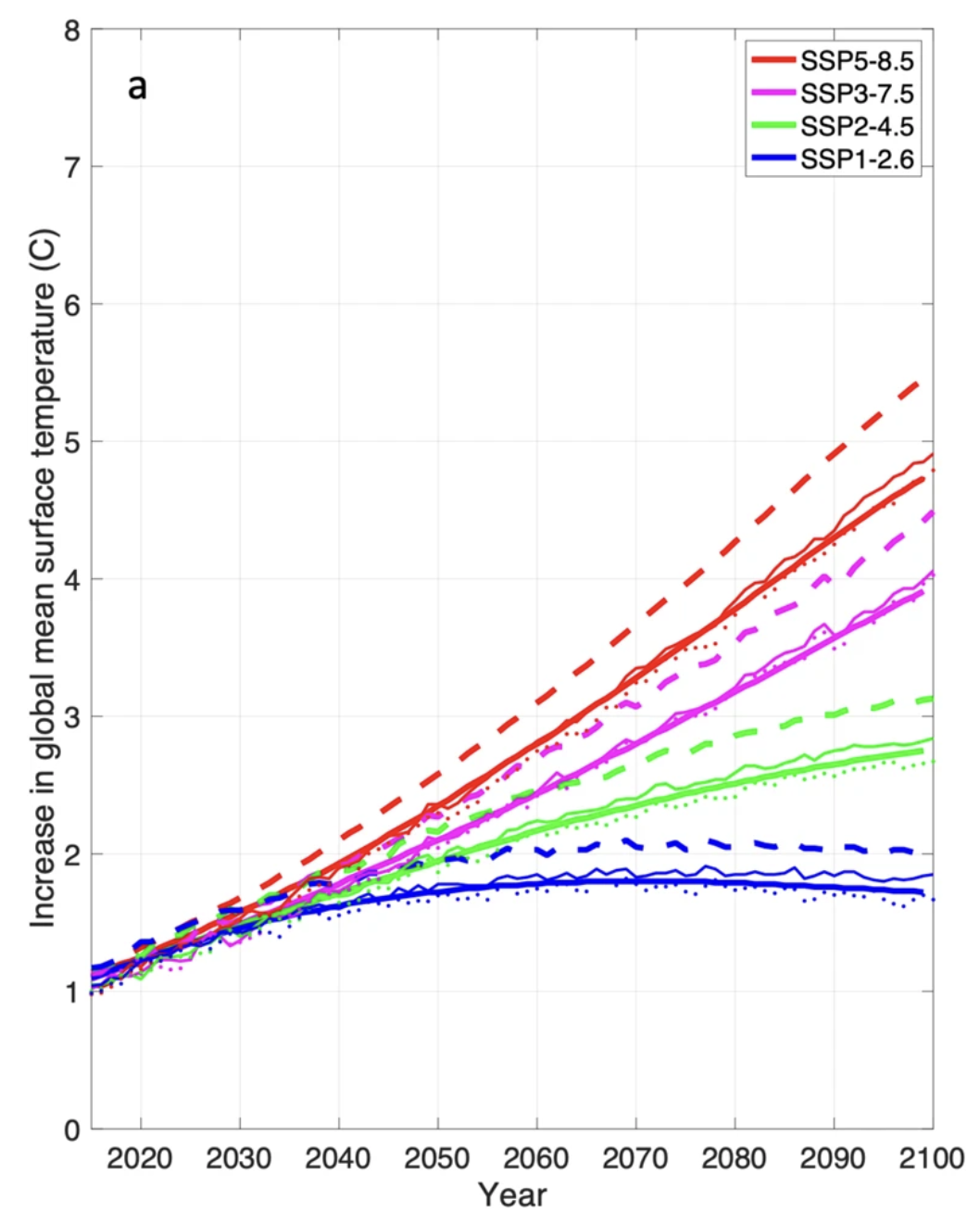
Using climate model ensembles containing members that exhibit very high climate sensitivities to increasing CO2 concentrations can result in biased projections. Various methods have been proposed to ameliorate this ‘hot model’ problem, such as model emulators or model culling. Here, we utilize Bayesian Model Averaging as a framework to address this problem without resorting to outright rejection of models from the ensemble. Taking advantage of multiple lines of evidence used to construct the best estimate of the earth’s climate sensitivity, the Bayesian Model Averaging framework produces an unbiased posterior probability distribution of model weights.
SSP: "Shared" Socioeconomic Pathways
[Note the scare quotes: climate outcomes are "shared" in the same manner as the financial burden and the human death toll of wars are shared.]
[From the Arbital guide]
Bayes' rule or Bayes' theorem is the law of probability governing the strength of evidence — the rule saying how much to revise our probabilities (change our minds) when we learn a new fact or observe new evidence.
You may want to learn about Bayes' rule if you are:
EXTRA: Here's how a classification problem can be reformulated as a regression problem.
Consider the case of two classes, \({\cal C}_1\) and \({\cal C}_2\). The posterior probability for class \({\cal C}_1\) can be written as $$ \begin{align} p({\cal C}_1\mid \textbf{x}) &= \frac{p(\textbf{x}\mid {\cal C}_1) p({\cal C}_1)}{p(\textbf{x}\mid {\cal C}_1)p({\cal C}_1) + p(\textbf{x}\mid {\cal C}_2)p({\cal C}_2)} \\ &= \frac{1}{1+exp(-a)} = \sigma(a) \end{align} $$ where \(a\) is the log likelihood ratio $$ a = \ln \frac{p(\textbf{x}\mid {\cal C}_1)p({\cal C}_1)}{p(\textbf{x}\mid {\cal C}_2)p({\cal C}_2)} $$ and \(\sigma(a)\) is the logistic sigmoid function, defined by $$ \sigma(a) = \frac{1}{1+exp(-a)} $$
Now let's assume that the class-conditional densities are \(D\)-dimensional Gaussian with the same covariance matrix \(\Sigma\): $$ p(\textbf{x}\mid {\cal C}_k) = \frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} exp\left\{-\frac{1}{2} (\textbf{x} -\mu_k)^{T} \Sigma^{-1} (\textbf{x} -\mu_k)\right\} $$ For two classes, \(k=2\), the expression for \(p({\cal C}_1\mid \textbf{x})\) from the previous slide yields: $$ p({\cal C}_1\mid \textbf{x}) = \sigma(\textbf{w}^{T}\textbf{x} + w_0) $$ where $$ \textbf{w} = \Sigma^{-1}(\mu_1 - \mu_2) $$ and $$ w_0 = - \frac{1}{2} \mu_1^{T} \Sigma^{-1} \mu_1 + \frac{1}{2} \mu_2^{T} \Sigma^{-1} \mu_2 + \ln\frac{p({\cal C}_1)}{p({\cal C}_2)} $$
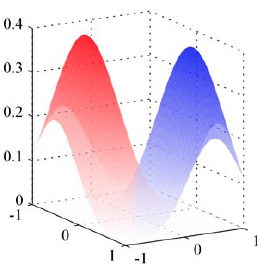
CLASSIFICATION reformulated as REGRESSION: $$ p({\cal C}_1\mid \textbf{x}) = \sigma(\textbf{w}^{T}\textbf{x} + w_0) $$
The quadratic terms in \(\textbf{x}\) from the exponents of the Gaussian densities have cancelled (due to the assumption of common covariance matrices) leading to a linear function of \(\textbf{x}\) in the argument of the logistic sigmoid.
Top: the class-conditional densities for two classes,
red and blue.
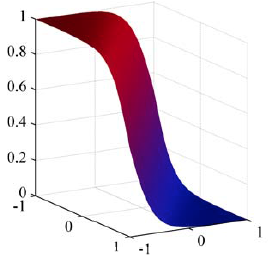
Bottom: the corresponding posterior probability \(p({\cal C}_1\mid x)\), given by a logistic sigmoid of a linear function of \(\textbf{x}\). The surface on the right is colored using a proportion of red ink given by \(p({\cal C}_1\mid \textbf{x})\) and a proportion of blue ink given by \(p({\cal C}_2\mid \textbf{x}) = 1 - p({\cal C}_1\mid \textbf{x})\).
Last modified: Wed Feb 5 2025 at 16:29:16 EST